

In our example if we divided the employees only according to their age, then we would have ignored the effect of gender on stress which would then accumulate with the experimental error.īut we divided them not only according to age but also according to gender which would help in reducing the error - this is application of the principle of local control for reducing error variation and making the design more efficient.
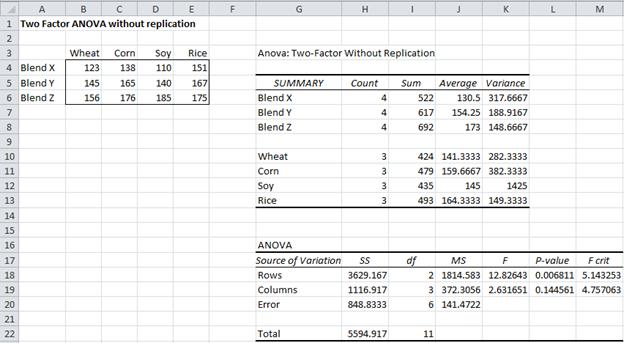
The principle of local control means to make the observations as homogeneous as possible so that error due to one or more assignable causes may be removed from the experimental error. Principles of replication and randomization need to be satisfied in a manner similar to One-Way ANOVA. Replication, Randomization and Local ControlĪn Two-Way ANOVA satisfies all three principles of design of experiments namely replication, randomization and local control. The only restriction is that the number of observations in each cell has to be equal (there is no such restriction in case of one-way ANOVA). Factor B is the brand of popcorn: gourmet versus national brand versus generic. Factor A is the type of popper: oil-based versus air-based. One can also test for independence of the factors provided there are more than one observation in each cell. Two-Way ANOVA (with replication) Suppose you want to compare type of popcorn popper and brand of popcorn with respect to their yield (in terms of cups of popped corn).Unlike One-Way ANOVA, it enables us to test the effect of two factors at the same time.There are two assignable sources of variation - age and gender in our example - and this helps to reduce error variation thereby making this design more efficient. Minitab - basic two-way analysis of variance using the General Linear Model (I use this option instead of the two-way so that if you do have a third factor or categorical variable it is simple to. An important advantage of this design is it is more efficient than its one-way counterpart.The assumptions in both versions remain the same - normality, independence and equality of variance. The computational aspect involves computing F-statistic for each hypothesis. H 03: The two factors are independent or that interaction effect is not present.In the second version, a third hypothesis is also tested: H 02: Both the gender groups have equal stress on the average.H 01: All the age groups have equal stress on the average.In the basic version there are two null hypotheses to be tested. This helps us to know if age and gender are independent of each other - they are independent if the effect of age on stress remains the same irrespective of whether we take gender into consideration. The advantage of the second version is it also helps us to test if there is any interaction between the two factors.įor instance, in the example above, we may be interested to know if there is any interaction between age and gender. The second version has more than one observation per cell but the number of observations in each cell must be equal. The basic version has one observation in each cell - one occupational stress score from one employee in each of the six cells. There are two versions of the Two-Way ANOVA.


 0 kommentar(er)
0 kommentar(er)
